Table I shows the results for each of the 12 separate databases, indicating the location, the persons responsible, and the
type of random event generator, followed by the number of trials, the Chisquare, its degrees of freedom, and the associated probability. The last line of the table shows the composite chisquare and probability for all 12 datasets.
Table I: Princess Diana, 12 Datasets | Location | Operator | Source* | N-Trials | Chisq | df | p-value |
|---|
| Princeton |
RN |
MicroREG 1 |
28438 |
7.417 |
4 |
0.115 |
| Princeton |
YD |
MicroREG 2 |
28362 |
3.948 |
4 |
0.413 |
| Princeton |
AL |
MicroREG 3 |
28462 |
12.900 |
4 |
0.012 |
| Princeton |
Cont. |
PortREG 6 |
26330 |
6.698 |
4 |
0.153 |
| Freiburg |
HB, EB |
PortREG 24 |
27976 |
5.386 |
4 |
0.250 |
| Freiburg |
HB, EB |
PortREG 26 |
27976 |
7.694 |
4 |
0.104 |
| Florida |
GS, LR |
PortREG 34 |
27978 |
0.993 |
4 |
0.911 |
| Chicago |
JW |
PortREG 36 |
27980 |
6.387 |
4 |
0.172 |
| Giessen |
JH |
PortREG 20 |
77 |
3.527 |
4 |
0.474 |
| Giessen |
JH |
PortREG 21 |
77 |
3.537 |
4 |
0.472 |
| Giessen |
JH |
FREMM |
775 |
6.369 |
4 |
0.173 |
| Las Vegas |
DR |
FREMM |
3829 |
7.612 |
4 |
0.107 |
|
| Total |
|
|
|
72.468 |
48 |
0.013 |
* Random sources include two independent designs for random event generators from the PEAR lab, the PortREG and MicroREG, and a third independent design (FREMM) by Dick Bierman and Joop Houtkooper of Amsterdam.
Figure 1 shows the accumulating chisquare over the 12 independent recordings during the ceremonies for Princess Diana, compared with its expectation and with a curve describing the locus of a significant deviation (p = 0.05) as the database grows. Because most of the individual Chisquare increments are larger than the expected value defined by the degrees of freedom, the cumulative curve takes on a definite trend culminating in a probability of 0.013.
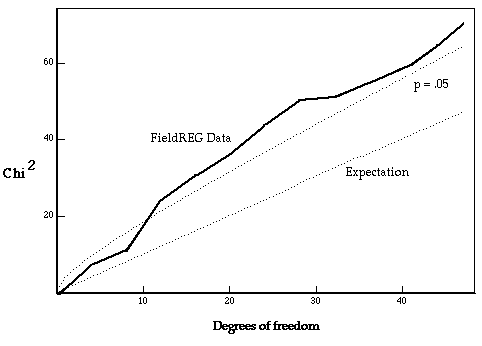
Figure 1: Cumulative squared deviation, or Chisquare, of the 12 independent recordings of data during the funeral ceremonies for Princess Diana. Each Chisquare has four degrees of freedom, and the cumulative trend is compared against expectation and against a 95% confidence envelope. See text for more detail.
The near coincidence of the funeral of Mother Teresa with that of Diana led to another FieldREG recording for this occasion, with essentially the same procedures. All but one of the contributors were able to provide data, and 11 independent records were obtained. Information available for specifying the active segments was less detailed, and in this case only two segments were defined, although the total time was similar for both funerals. As detailed in Table II, the results in this case show little indication of an anomalous effect, and the composite outcome is indistinguishable from chance.
Table II: Mother Teresa, 10 Datasets | Location | Operator | Source* | N-Trials | Chisq | df | p-value |
|---|
| Princeton |
RN |
MicroREG1 |
26808 |
0.074 |
2 |
0.964 |
| Princeton |
YD |
MicroREG2 |
26701 |
1.919 |
2 |
0.383 |
| Princeton |
AL |
MicroREG3 |
26824 |
0.015 |
2 |
0.992 |
| Princeton |
Cont. |
PortREG6 |
24814 |
2.630 |
2 |
0.268 |
| Freiburg |
HB, EB |
PortREG24 |
26364 |
3.314 |
2 |
0.191 |
| Freiburg |
HB, EB |
PortREG26 |
26365 |
0.120 |
2 |
0.942 |
| Tucson |
GS, LR |
PortREG34 |
26367 |
2.003 |
2 |
0.367 |
| Giessen |
JH |
PortREG20 |
72 |
1.461 |
2 |
0.482 |
| Giessen |
JH |
PortREG21 |
72 |
4.010 |
2 |
0.135 |
| Giessen |
JH |
FREMM |
720 |
2.696 |
2 |
0.260 |
| Las Vegas |
DR |
FREMM |
3609 |
0.743 |
2 |
0.690 |
|
| Total |
|
|
|
19.004 |
22 |
0.645 |
Figure 2 shows the accumulating chisquare over the 11 independent recordings at the ceremonies for Mother Teresa, using the same format as in Figure 1. In this case, the accumulating Chisquare values do not take on a trend relative to expectation.
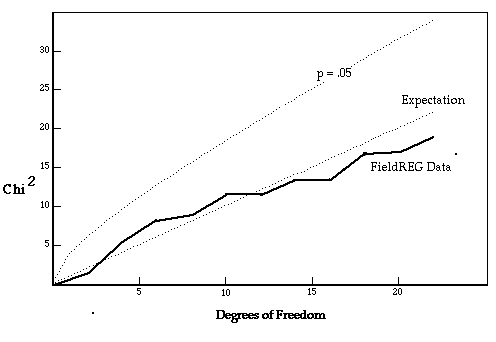
Figure 2: Cumulative squared deviation, or Chisquare, of the 11 independent recordings of data during the funeral ceremonies for Mother Teresa. Each Chisquare has two degrees of freedom, and the cumulative trend is compared against expectation and against a 95% confidence envelope. See text for more detail.
Graphs of the individual random walks described by the data from the 12 recordings during Diana's funeral show strong, highly variable excursions, some of which coincide with the defined analytical segments, resulting in large contributions to the Chisquare. If all the traces are averaged, the resulting graph shows a consistent negative trend for the first four hours, including a relatively strong portion during the ceremonies at Westminster Abbey. About an hour later, the averaged data take on a positive trend that brings the cumulative deviation back to expectation. In contrast, the random walks described by the 11 datasets recorded during the ceremonies for Mother Teresa generally exhibit smaller deviations. An average across the traces is striking for its close adherence to the straight line of theoretical expectation.

